Die Berechnung der Transmissionswärmeverluste eines Gebäudes erschöpfen sich nicht in der aufwendigen Flächenermittlung und der Berechnung der U-Werte mit allen Korrekturen durch Dämmstoff- oder Fassadenhalter, Gefälledämmungen, Luftspalte und andere Einflüsse. KfW-Prüfer haben übrigens ein Auge darauf. Basis für die Berechnung der Transmissionswärmeverluste ist die DIN EN ISO 6946, auch gegen Erdreich ist daraus die Berechnung des Wärmedurchgangswiderstands notwendig.
Gemäß Gebäudeenergiegesetz (GEG) müssen heute alle Energiebilanzen von Gebäuden mit der DIN V 18599 von 2018 [1] gerechnet werden, die Transmissionswärmeverluste sind in Teil 2 der Norm erläutert. (Hinweis: Seit 10/2025 gibt es eine Neufassung der Norm, auf die sich vermutlich die künftige Fassung des Gebäudeenergiegesetzes bezieht). Dort wird klar formuliert: „Der Wärmetransferkoeffizient HT, j ist aus den Wärmedurchgangskoeffizienten der einzelnen Bauteile und deren Flächen nach DIN EN ISO 13789 und DIN EN ISO 13370 unter Berücksichtigung linienförmiger Wärmebrücken zu ermitteln. Vereinfachend können die Wärmebrücken pauschal angesetzt werden.“
Damit wird an zentraler Stelle in Abschnitt 5.3.2 auf die beiden weniger im Fokus stehenden ISO-Normen 13370 [2] und 13789 [3] verwiesen. Letztere regelt, dass ein U-Wert nach DIN EN ISO 6946 [4] für Flächen gegen Außenluft oder die gegen eine Temperatur in der angrenzenden (unbeheizten) Zone zu berechnen ist. Dies gilt auch für beheizte oder gekühlte Zonen, die in der Praxis jedoch häufig vernachlässigt werden. Die Verluste gegen Erdreich oder unbeheizte Keller sollen dagegen nach DIN EN ISO 13370 ermittelt werden.
Ein vereinfachter Ansatz in DIN V 18599-2 in Abs. 6.1.4.2 mit den Tabellen 5 und 6 führt – nur für den Heizfall – Reduktionsfaktoren auf, mit der die Temperaturdifferenz zwischen innen und außen reduziert werden kann. Das Problem ist, dass im Kühlfall diese Reduktionsfaktoren nicht passen, weil dann teilweise auch deutlich höhere Temperaturen als die Außentemperaturen herrschen können, beispielsweise in Abseiten- oder Dachräumen. Auch hierfür gibt es vereinfachte Ansätze. Für die Transmission über das Erdreich dürfen diese Reduktionsfaktoren (Fx-Werte) indes nur angesetzt werden, wenn das Gebäude ungekühlt ist (Abs. 6.2.4), ansonsten muss der Wärmetransferkoeffizient HT,s aus der ISO 13370 verwendet werden. Dies wird für Förderprogramme auch in den technischen FAQ der KfW in Punkt 4.07 bestätigt.
Demnach müssen die Transmissionswärmeverluste für alle Gebäude, die mit reversiblen Wärmepumpen ausgestattet werden – also eine Vielzahl aktueller Projekte – mit dem aufwändigeren ISO-Verfahren berechnet werden. Dies gilt gemäß Definition des Gebäudeenergiegesetzes auch für freie Kühlung, also reine Sondenkühlung von Sole-Wasser-Wärmepumpen. Wichtiger Hinweis am Rande: Ohne Nachweis einer Unwirtschaftlichkeit muss auch für gekühlte Gebäude immer der sommerliche Wärmeschutz nach DIN 4108-2 eingehalten werden.
Korrekte Berechnung zum Erdreich
Grundlagen
In der Berechnung der Wärmeverluste gegen Erdreich wird gemäß dem deutschen nationalen Anhang zur ISO 13370 das Erdreich standardmäßig mit einer Wärmeleitfähigkeit von 2 W/(m²K) angesetzt, fließendes Grundwasser vernachlässigt und der kälteste Monat ist der Januar. Und nun geht es los: Die Berechnung des Wärmedurchgangswiderstandes verweist dafür auf ISO 6946, fordert jedoch dabei auch die Berücksichtigung der feuchte- und temperaturbedingten Wärmeleitfähigkeiten. Entsprechende Daten sind jedoch nur bedingt verfügbar. Für die hierzu geeigneten Dämmstoffe ist entsprechend Anwendungsfall aus der Zulassung der korrekte Wert zu wählen, der nicht unbedingt dem erstbesten Katalogwert entspricht. Wer das richtig macht, ist auf einem guten Weg.
Das Prinzip ist nun, dass äquivalente U-Werte gegenüber der Außenluft über Keller und/oder Erdreich berechnet werden. Ebenso werden „wirksame Dicken“ der Bauteile gegen Erdreich und gegebenenfalls der Randdämmung ermittelt.
Ein zentraler Wert für die Berechnung ist das Flächen- (A) zu Umfang- (Perimeter P) Verhältnis, also das Bodenplattenmaß B, das den mittleren Abstand aller Punkte eines unteren Abschlusses zur Erdoberfläche neben dem Gebäude über die Breite eines quasi unendlich langen Gebäudes auf einen zweidimensionalen Fall einer Bodenplatte reduziert:
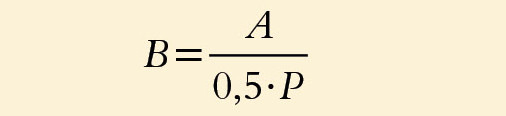
Berechnungsfälle
Für die konkrete Berechnung werden folgende Bauarten beziehungsweise Berechnungsfälle unterschieden:
Der letzte Fall ist noch relativ einfach zu beschreiben: ein flächengewichteter Durchschnittswert der Wärmeverluste über Erdreich aus einer Berechnung für einen voll beheizten und einen unbeheizten Keller.
Die Berechnungen sind alle nicht ganz einfach – und praktisch nur mit entsprechenden Berechnungswerkzeugen umsetzbar, am besten in der jeweils genutzten Energieberatersoftware. Im Haupttext der Norm wird die Berechnung des stationären Anteils der Wärmeverluste beschrieben. Dies ist jedoch nicht alles. Dazu kommen die Wärmebrückenverluste aufgrund möglicher Randdämmungen (vgl. Abb. 1, geregelt in Anhang D; siehe auch Infokasten 1) sowie die jährliche periodische Wärmestromvarianz aufgrund der Trägheit des Erdreichs, gemäß Anhang C und H. Vereinfacht kann in nicht klar definierten Fällen gemäß C.5 auch auf die Berücksichtigung der periodischen Schwankungen verzichtet werden. Logisch wäre, dass dies die Fälle betrifft, die auch vereinfacht mit den Fx-Faktoren berechnet werden können, nicht jedoch gekühlte Gebäude.
Für den stationären Anteil mit Randdämmung ergibt sich die Berechnung scheinbar bekannt zu
Hg = A ∙ U + P ∙ ψwf
Da es in diesem Artikel zu weit führen würde, dies alles im Detail zu erläutern, beschränkt sich das nachfolgende Beispiel auf eine anschauliche Bodenplatte. Und, um den Effekt besonders deutlich zu zeigen, auf eine ungedämmte Platte in einer Effizienzhaus-40-Sanierung.
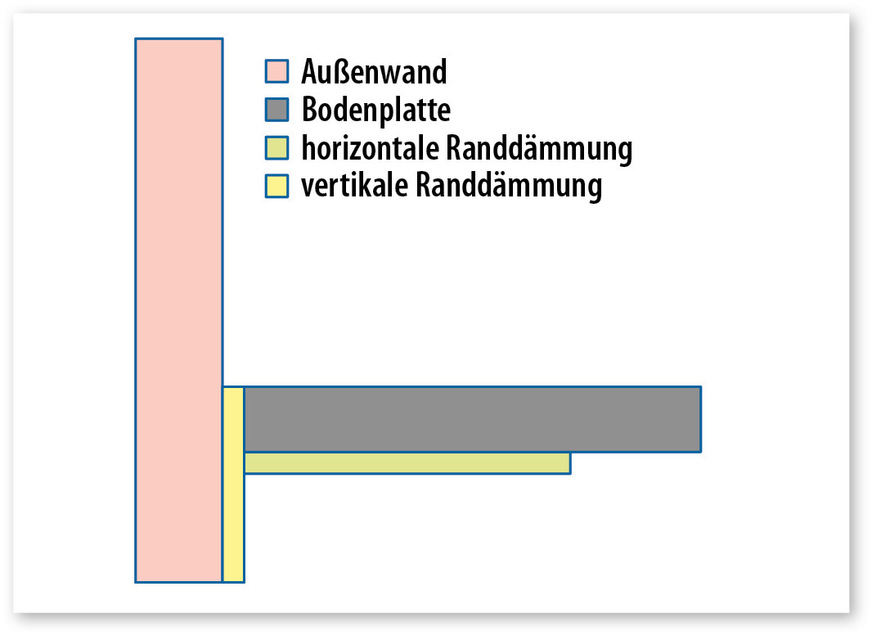
Bild: Energiebuendel
Rechenbeispiel Bodenplatte
Schon die Berechnung des stationären U-Wertes wird etwas komplizierter. Für den Fall der Bodenplatte mit Ufg,sog gibt es zwei Formeln, je nach Dämmniveau der Bodenplatte. Etwas ähnliches ist auch aus der Tabelle 6 mit Fx-Werten gegen Erdreich in [1] bekannt.
Dazu muss zuerst die wirksame Dicke df der Bodenplatte berechnet werden:
df = dw,e + λg ∙ (Rsi + Rf,sog + Rse)
Wärmedurchlasswiderstand der inneren bzw. äußeren Oberfläche, in [(m²K)/W].
Man sieht, die Definitionen weichen teilweise leicht von den üblichen Definitionen ab, wenn bei Wohngebäuden Bodenbeläge berücksichtigt werden sollten. Darauf sollte aus Gründen der Einfachheit und Vergleichbarkeit verzichtet werden.
Diese wirksame Dicke wird nun mit dem Bodenplattenmaß B verglichen. Wenn die wirksame Dicke df kleiner als das Bodenplattenmaß ist, wie im ungedämmten Beispiel, gilt für den U-Wert der Bodenplatte Ufg,sog:
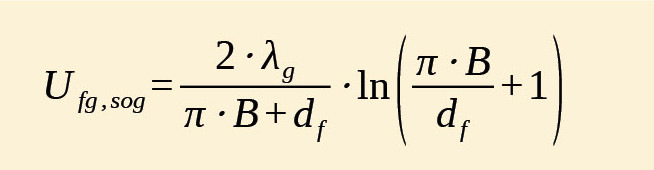
Etwas einfacher wäre es in diesem Fall, wenn die Bodenplatte gut gedämmt ist:
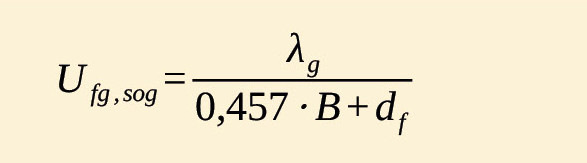
Diese Werte können für Berechnungen nach DIN V 18599-2, Kap. 6.4.2 immer genutzt werden, soweit die Wärmeströme über Erdreich nicht „erheblich“ sind. So unklar ist die Norm. Doch was heißt nun „erheblich“? Aus Sicht des Autors wäre spätestens dann davon auszugehen, wenn mehr als 30 Prozent der Wärmeströme über das Erdreich gehen. Dies kann vor allem bei ungedämmten Bodenplatten in Effizienzhaussanierungen oder ansonsten gut gedämmten Nichtwohngebäuden der Fall sein, zum Beispiel bei befahrbaren, jedoch thermisch konditionierten Hallen.
Instationäre Wärmeströme über das Erdreich
Für den harmonischen Anteil gestaltet sich die Berechnung komplexer (siehe Infokasten 2). Das Prinzip ist, dass ein sinusförmiger Verlauf der Innen- und Außentemperatur angenommen wird (Abb. 2) und daraus monatliche Zu- oder Abschläge über zusätzliche innere und äußere Wärmetransferkoeffizienten auf den stationären Wärmeverlust addiert werden.
Beispiel Effizienzhaus-Sanierung
Ein typischer Fall für eine derartige Berechnung ist eine Mehrfamilienhaus-Sanierung eines Gebäudes von 13,33 mal 20 Meter Grundfläche und beispielsweise 2,5 Geschossen mit acht Wohn-
einheiten, gegründet auf einer ungedämmten Bodenplatte. Die Beheizung erfolgt über eine reversible Luft-Wasser-Wärmepumpe, die im Sommer auch kühlt. Mit dieser etwas krummen Geometrie ergibt sich ein Bodenplattenmaß von genau acht Metern.
Zur Reduktion des Wärmebrückeneffekts wird vor das Streifenfundament eine 70 cm hohe und zehn Zentimeter dicke Perimeterdämmplatte gestellt (im Beispiel waren es zwei Platten à 50 cm, wobei die oberen 30 cm im Spritzwasserbereich über Erdreich liegen), die eine Wärmeleitfähigkeit von 0,040 W/(m²K) aufweist.
Dafür ergeben sich nach den in Infokasten 2 beschriebenen Berechnungen Ergebnisse für die monatlichen Wärmeströme über die Bodenplatte nach Abb. 3, wobei darin jeweils unterschieden wird zwischen
Man sieht, dass die Jahressummen gleich sind, die Wärmeverluste über die Bodenplatte über das Jahr verteilt jedoch deutlich variieren.
Wenn man dies noch mit den ungefähren Heiztagen (graue Balken) multipliziert, die sich aus einer Berechnung nach DIN V 18599-2 ergeben, kommt man für die Heizperiode auf die Werte aus Abb. 4. Demzufolge werden, basierend auf dem Gesamtwärmestrom über die Bodenplatte im Jahr mit Berücksichtigung der dynamischen Heizlastanteile, nur etwa 70 Prozent des Wärmestroms in der Heizzeit angerechnet. Ohne diese dynamischen Anteile sind es 90 Prozent, womit man natürlich auf der sicheren Seite liegt, falls die genutzte Software die dynamischen Anteile nicht abbilden kann.
Im Vergleich dazu ergibt sich ein Jahresgesamtwärmestrom über die Bodenplatte ohne Wärmebrücken von 175 Prozent nach der gängigen Rechenmethode mit dem FX-Wert von 0,2 in diesem Beispiel, weil die Randdämmung keine zwei Meter senkrecht ist und damit nicht angerechnet werden kann.
Bild: Energiebuendel
Bild: Energiebuendel
Bild: Energiebuendel
3 Berechneter monatlicher Wärmestrom durch die Bodenplatte ins Erdreich mit (rot) und ohne (gelb) dynamische Anteile
4 Berechneter monatlicher Wärmestrom durch die Bodenplatte ins Erdreich mit (rot) und ohne (gelb) dynamische Anteile für die Heizzeit, wobei die anzusetzenden Heiztage (graue Balken) vom konkreten Gebäude abhängen. Hier wurde für die Grenzmonate Mai und September ein ungefährer Wert angesetzt.
Die Konsequenzen für die Energiebilanz
Dadurch ergeben sich in der Summe des Jahresverlaufs für die statische und dynamische Berechnung keine wesentlich unterschiedlichen Wärmeströme, jedoch verschieben sich die Wärmeströme über die Monate. Das führt im Sommer zu eher höheren Wärmeströmen über die Bodenplatte ins Erdreich, im Winter dagegen zu geringeren. Somit verändern sich auch Heiz- und Kühllasten und die entsprechenden Energien, was wiederum die Ursache für den notwendigen Ansatz dieser periodischen Wärmeströme bei Kühlung ist. Als Nebeneffekt erleichtert diese Berechnungsmethode auch das Ziel, Sanierungen zum Effizienzhaus-40 zu schaffen.
Die dafür notwendigen detaillierten Wärmebrückenberechnungen gestalten sich allerdings bei den erdberührten Bauteilen ebenfalls komplizierter: Die Berechnung nach Beiblatt 2 wird untauglich und führt zu krassen Fehlern, da diese auch die Ansätze der Fx-Werte in der Fläche voraussetzen. Die zur hier erläuterten Wärmestromberechnung in der Fläche passende Wärmebrückenberechnung nach DIN EN ISO 10211 wird im zweiten Teil des Artikels beleuchtet.
Der Autor sammelt gerne Hinweise, welche Software die DIN EN ISO 13370 nicht, teilweise oder ganz abbilden kann. Auch interessiert ihn, ob eine Software das Bodenplattenmaß als Innenmaß erfasst. Hinweise gerne an: info@energiebuendel.com.
Literatur und Quellen
[1] DIN V 18599: Energetische Bewertung von Gebäuden – Berechnung des Nutz-, End- und Primärenergiebedarfs für Heizung, Kühlung, Lüftung, Trinkwarmwasser und Beleuchtung – Teil 2: Nutzenergiebedarf für Heizen und Kühlen von Gebäudezonen, Beuth-Verlag, Berlin, September 2018
[2] DIN EN ISO 13370: Wärmetechnisches Verhalten von Gebäuden – Wärmetransfer über das Erdreich – Berechnungsverfahren, Beuth-Verlag, Berlin, März 2018
[3] DIN EN ISO 13789: Wärmetechnisches Verhalten von Gebäuden – Transmissions- und Lüftungswärmetransferkoeffizient – Berechnungsverfahren, Beuth-Verlag, Berlin, April 2018
[4] DIN EN ISO 6946: Bauteile – Wärmedurchlasswiderstand und Wärmedurchgangskoeffizient – Berechnungsverfahren, Beuth-Verlag, Berlin, April 2008 bzw. März 2018. Hinweis: Hier wird im GEG auf die Version von 2008 verwiesen!
[5] Wärmeverluste durch das Erdreich; Protokollband Nr. 27 des Arbeitskreises kostengünstige Passivhäuser, 1. Auflage, Passivhaus Institut, Darmstadt 2004
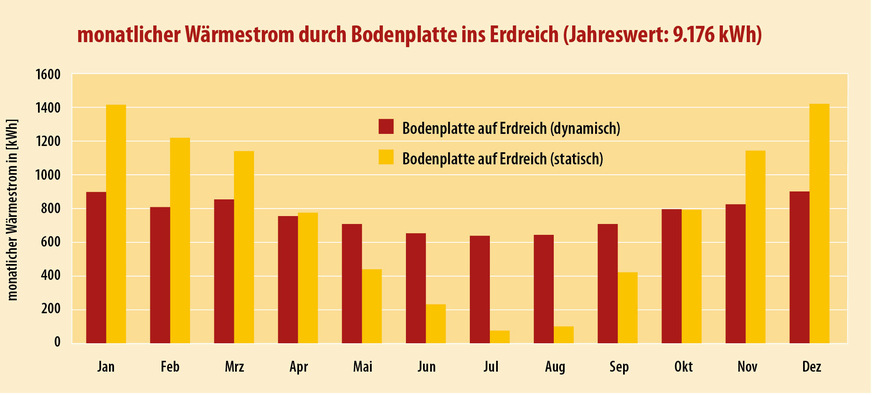
Bild: Energiebuendel
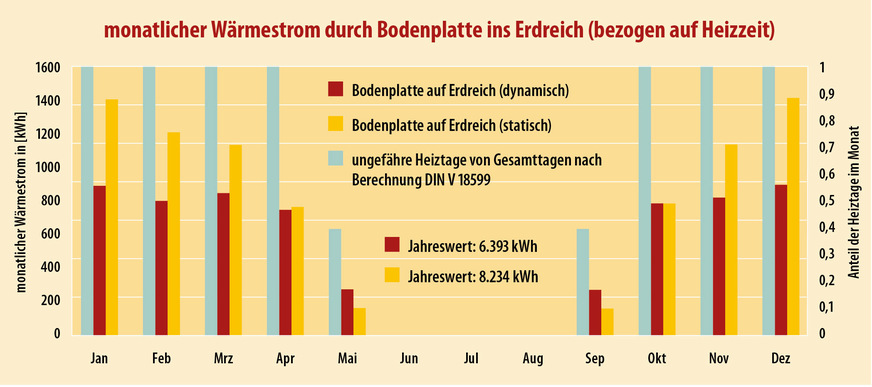
Bild: Energiebuendel
Kurz und knackig
Der Artikel macht deutlich, dass Transmissionswärmeverluste von Gebäuden insbesondere gegen Erdreich nach GEG und DIN V 18599 häufig zu vereinfacht berechnet werden. Für erdberührte Bauteile ist grundsätzlich die DIN EN ISO 13370 maßgeblich. Vereinfachte Fx‑Reduktionsfaktoren dürfen nur bei ungekühlten Gebäuden eingesetzt werden. Bei Gebäuden mit Kühlung oder reversiblen Wärmepumpen ist das detaillierte ISO‑Verfahren zwingend anzuwenden, was auch die KfW fordert. Der Beitrag erläutert die normativen Grundlagen, relevante Berechnungsfälle von Bodenplatten und Kellern sowie die Bedeutung des Bodenplattenmaßes. Neben stationären Wärmeverlusten sind Wärmebrücken und instationäre, periodische Wärmeströme des Erdreichs zu berücksichtigen. Ein Sanierungsbeispiel zeigt, wie sich diese dynamischen Anteile auf die Verteilung von Heiz‑ und Kühlenergie auswirken und warum vereinfachte Ansätze die Energiebilanz deutlich verfälschen können.
Infokasten 1: Besonderheiten bei der Definition Bodenplatte
Interessant ist, dass die Wände gemäß der Logik der ISO 13370 außerhalb der Bodenplatte sind. Die Bodenplatte hat einen Innenmaßbezug in der Norm, liegt also zwischen den Wänden. Entsprechend trennen Randdämmungen die Bodenplatte gegenüber dem Erdreich (horizontal) oder gegenüber der Wand (vertikal, Abb. 1). Das Bodenplattenmaß bezieht sich also auf die Grundfläche ohne Außenwände. In der Praxis ist dem Autor keine Software bekannt, die das Bodenplattenmaß so ermittelt – die meisten Programme nehmen wie überall den Außenmaßbezug als Grundlage. Auch das Passivhaus-Institut wählt diese Vorgehensweise [5]. Der Fehler durch den Außenmaßbezug im Vergleich zum Normmaßbezug ist in der Regel aber vernachlässigbar. Außerdem entspricht die Trennung zwischen Außenwand und Bodenplatte auch nicht der hierzulande gebauten Realität.
Infokasten 2: Berechnung des dynamischen, instationären Wärmestroms
Die Berechnungen des instationären Anteils bei erheblichen Wärmeverlusten über Erdreich werden in den normativen Anhängen C und H der Norm ISO 13370 beschrieben. Für die Berechnung gibt es durch den Verweis in der DIN V 18599-2 auf das zu verwendende Φm zwei monatsweise Ansätze in C.2 und C.3. Dieses Rechenbeispiel erläutert die einfachere Variante über monatliche Mitteltemperaturen aus C.3.
Φm als mittlerer Wärmestrom (in W) in Monat m (1 bis 12) wird demnach aus vier Termen summiert:
dem statischen Anteil des Wärmeverlusts über Erdreich mit den Jahresmittelwerten der Temperaturen;
dem Wärmeverlust über den Wärmebrückenverlust am Perimeter mit den Monatsmittelwerten der Temperaturen;
einem Abzug für den inneren periodischen Wärmestromanteil Hpi für die Differenz der inneren Jahresmitteltemperatur minus der iterativ berechneten, inneren Monatsmitteltemperatur aus der 18599-Berechnung;
plus dem äußeren periodischen Wärmestromanteil Hpe für die Differenz der äußeren Jahresmitteltemperatur minus der äußeren Monatsmitteltemperatur aus dem Wetterdatensatz.
Die Temperaturen werden dabei prinzipiell sinusförmig über das Jahr gemäß Abb. 2 angenommen. Die Berechnungen der periodischen Wärmestromanteile H werden in Anhang H erläutert. Es werden für die im Artikel genannten, verschiedenen Fälle Berechnungswege für jeweils Hpi und Hpe aufgeführt, also die inneren und äußeren dynamischen Wärmeströme am Perimeter. Außerdem wird für die Bodenplatte auf Erdreich unterschieden zwischen
keiner Randdämmung, also voll- oder ungedämmt und
mit Randdämmung.
Die Berechnungsformeln für Bodenplatten ohne Randdämmung – ausgehend von in die Formeln eingesetzten Standardwerten für Erdreich, die sich auf Sand oder Kies in der Norm ISO 13370 beziehen – lauten demnach:

Hpi innerer periodischer Wärmestromanteil, in [W/K]
A Fläche der Bodenplatte, in [m2]
df wirksame Gesamtdicke der Bodenplatte, in [m]
und

Hpe äußerer periodischer Wärmestromanteil, in [W/K]
P Umfang, in [m]
df wirksame Gesamtdicke der Bodenplatte, in [m]
Die inneren periodischen Wärmestromanteile hängen also stärker von der Fläche der Bodenplatte ab, außen hingegen vom Umfang. Das gilt für alle in der Norm dargestellten Fälle.
Für die vier anderen Fälle sind die Formeln deutlich komplizierter. Gerechnet wurde für das Beispiel im Artikel (Abb. 3 und 4) mit den Formeln für Bodenplatte mit senkrechter Randdämmung. Außerdem sind aus Anhang D die Formeln für die reduzierten Wärmebrückenverluste durch die Randdämmung der Bodenplatte in diese Berechnung mit eingeflossen. Diese müssen in den stationären Leitwert und können bei Bedarf auch in den äquivalenten Ufg,sog-Wert eingerechnet werden.